Diracovo delta
funkce, která má v jednom bodě hodnotu nekonečno a v ostatních je identická nule
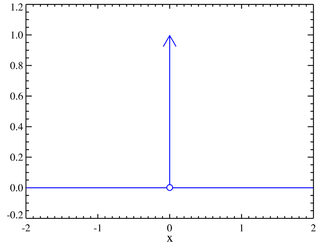
Diracovo delta nebo Diracova -funkce se dá neformálně popsat jako funkce, která má v nule hodnotu nekonečno a všude jinde nulovou. Je značena řeckým písmenem delta. Její integrál přes celý prostor je roven jedné.

- , kde H znamená Heavisideovu funkci
V souvislosti se zpracováním signálu bývá Diracova funkce označována také jako Diracův jednotkový impuls. (Jednotkový právě pro integrál rovný jedné)
V exaktním matematickém popisu není Diracova delta funkcí, ale distribucí. Diskrétním ekvivalentem Diracova delta je Kroneckerovo delta.
Vyjádření
editovatDiracovu -funkci lze vyjádřit různými způsoby. Pro komplexní čísla například ve tvaru integrálu.
Nebo pomocí limit.
Vlastnosti
editovatOznačení posunuté („doprava“) delta funkce:
- Delta funkce je sudá funkce.
- Působí jako jednotkový operátor při integraci.
- Konvoluce libovolné funkce s delta funkcí je rovna této funkci.
- Konvoluce s posunutou delta funkcí má za následek posunutí této funkce.
- Fourierova transformace delta funkce je rovna jednotkové funkci.
- Z toho plyne, že zpětná Fourierova transformace jednotkové funkce je ve smyslu distribuce rovna delta funkci.
- Pro Fourierovu transformaci posunuté delta funkce platí:
- Je-li funkce s kořeny , platí:
- Další vztahy:
Odkazy
editovatReference
editovatSouvisející články
editovatExterní odkazy
editovat- Obrázky, zvuky či videa k tématu Diracovo delta na Wikimedia Commons
- Diracovo delta v encyklopedii MathWorld (anglicky)




