Reverzní Segnerovo kolo
Reverzní Segnerovo kolo je taková modifikace Segnerovy turbíny (klasického Segnerova kola), při níž pracovní tekutina (obvykle voda nebo vzduch) proudí celým systémem v opačném směru než u běžného Segnerova kola. Vstupuje tedy do trysek na obvodu turbíny zevně a teče směrem k ose rotace.
V komentáři k úlohám Turnaje mladých fyziků[1] je následující zmínka: „Nechyběla ani známá Feynmanova úloha o obráceném Segnerově kole, na kterou se studenti tak často ptají. Bude se Segnerovo kolo otáčet pod vodou při nasávání místo při vystřikování vody? A kterým směrem?“ Richard Feynman tuto úlohu skutečně zpopularizoval ve své knize,[2] konkrétně v kapitole věnované vzpomínkám na Princeton. Úlohu se svými studenty rozebíral teoreticky i experimentálně, postříkal přitom zařízení princetonské cyklotronové laboratoře, když mu praskl skleněný zásobník s vodou, ale žádné řešení nikdy nepublikoval. Nebyl však prvním, kdo se tomuto problému věnoval.
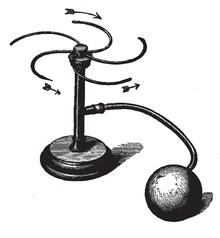
Koncem 19. století experimentoval Ernst Mach s laboratorním modelem zařízení, které nazval reakční kolo (Reactionsrad). Vzduch do svého reakčního kola foukal připojeným balonkem (kolo se roztočilo) nebo jej tímtéž balonkem v reverzním režimu vysával (pokud bylo kolo na začátku experimentu v klidu, v klidu zůstalo). Mach to vysvětloval tím, že při stlačení balonku je vzduch z trysek vyfukován ve formě paprsku jasně definovaným směrem, zatímco při nasávání vstupuje vzduch do obvodových trysek ze všech stran, a proto se kolo neroztočí.[3] Podobná pozorování později učinili nezávisle i jiní.[4][5]

Rozbor chování reverzního Segnerova kola, které je v klidu a protéká jím v ustáleném stavu ideální tekutina (kapalina nebo plyn bez vnitřního tření), ukazuje, že na takové kolo působí dva opačně orientované, co do velikosti však shodné silové momenty – kolo se tedy netočí. První silový moment souvisí se spádem tlaku uvnitř potrubí reverzního kola, druhý se silovým působením proudící tekutiny na vnitřní stěnu v oblouku potrubí. Kdyby tedy nebylo viskozity pracovní tekutiny, vykazovalo by reverzní kolo pouze přechodný krouticí moment v okamžiku zahájení průtoku a žádný krouticí moment v ustáleném stavu, což lze vysvětlit s použitím zákona zachování momentu hybnosti[6][7].
Existují i takové práce, podle nichž se reverzní kolo točí opačně než běžná Segnerova turbína, i když výrazně pomaleji. To se potom vysvětluje buď disipací energie reálné tekutiny v potrubí reverzního kola,[8][9] nebo tvorbou vírů uvnitř systému v oblasti přechodu pracovní tekutiny z rotoru do statoru, kterým se tekutina odsává ven. Tuto teorii podporuje zjištění, že k rotaci reverzního kola nedojde, pokud se tvorba vírů potlačí (např. jemnou síťkou uvnitř rotoru).[10][11] Rozbor chování reverzního Segnerova kola se započítáním všech jemných efektů, k nimž patří např. proudění viskózní pracovní tekutiny, zúžení toku za tryskami, disipace energie, působení Coriolisovy síly při rotaci, vliv vírů, úloha tření v uložení rotoru apod. představuje poměrně komplexní teoretický i experimentální problém.
Reference
editovat- ↑ ŠTOLL, Ivan. Zamyšlení nad úlohami Turnaje mladých fyziků. S. 322. Pokroky matematiky, fyziky a astronomie [online]. Jednota českých matematiků a fyziků, 1995 [cit. 2020-01-13]. Roč. 40, čís. 6, s. 322. Dostupné online.
- ↑ FEYNMAN, Richard P.; LEIGHTON, Ralph. Surely You’re Joking, Mr. Feynman!. New York: W. W. Norton and Company, 1985. Český překlad Jana Klímy: To snad nemyslíte vážně! Mladá fronta, Praha 1989.
- ↑ MACH, Ernst. Die Mechanik in ihrer Entwicklung historisch-kritisch dargestellt [online]. Leipzig: F. A. Brockhaus, 1897 [cit. 2020-01-13]. S. 294 – 297. Dostupné online.
- ↑ KIRKPATRICK, Paul. A Neglected Lesson from the Cartesian Diver. S. 160. American Journal of Physics [online]. 1942 [cit. 2020-01-12]. Roč. 10, s. 160. Dostupné online.
- ↑ BELSON, Henry S. “Empty” Hero's Engine. S. 413. American Journal of Physics [online]. 1956 [cit. 202-01-12]. Roč. 24, s. 413. Dostupné online.
- ↑ JENKINS, Alejandro. An elementary treatment of the reverse sprinkler. S. 1276. American Journal of Physics [online]. 2004 [cit. 2020-01-12]. Roč. 72, s. 1276. Dostupné online.
- ↑ JENKINS, Alejandro. Sprinkler head revisited: momentum, forces, and flows in Machian propulsion. S. 1213 – 1226. European Journal of Physics [online]. IOP Publishing, 5 July 2011 [cit. 2020-01-12]. Roč. 32, čís. 5, s. 1213 – 1226. Dostupné online.
- ↑ Feynman Sprinkler [online]. Fermat's Library, 2017-09-28 [cit. 2020-01-12]. Dostupné online.
- ↑ Inverse Sprinkler - Metal Model. Physics Lecture Demonstration Facility [online]. 28 Jul 2014 [cit. 2020-01-12]. Dostupné online.
- ↑ LANGER, Jan. Experimentální ověření chování reverzního Segnerova kola [online]. Praha: ČVÚT, Fakulta strojní, Ústav mechaniky tekutin a termodynamiky, 2019 [cit. 2020-01-10]. S. Počet stran 69. Bakalářská práce. Dostupné online.
- ↑ BEALS, Joseph. New angles on the reverse sprinkler: Reconciling theory and experiment. American Journal of Physics [online]. 2017 [cit. 2020-01-13]. Roč. 85, čís. 3. Dostupné online. DOI 10.1119/1.4973374.