Regulární jazyk

Regulární jazyky jsou nejjednodušší formální jazyky v rámci Chomského hierarchie. Regulární jazyky nad abecedou Σ lze zavést následujícím způsobem:

prázdný jazyk Ø je regulární.
pro každé a z abecedy, jazyk { a } je regulární.
pokud A a B jsou regulární jazyky, jsou A ∪ B (sjednocení), A • B (konkatenace), a A* (iterace) také regulární.
žádné další jazyky regulární nejsou.

O regulárních jazycích lze dokázat řadu tvrzení. Např. formální jazyk je regulární, právě když:

je akceptovaný nějakým deterministickým konečným automatem,
je akceptovaný nějakým nedeterministickým konečným automatem,
může být popsán regulárním výrazem nebo
může být vygenerován regulární gramatikou

Všechny konečné jazyky jsou regulární. Dalším příkladem je například jazyk nad abecedou {a, b} obsahující lichý počet symbolů a.

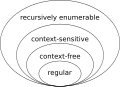
Všechny regulární jazyky jsou bezkontextové, ale ne všechny bezkontextové jazyky jsou regulární. Tomuto je možno snadno nahlédnout díky Chomského Hierarchii na obrázku:

To, že „Regulární => bezkontextový“ a ne vždy opačně, je možné vidět na obrázku Chomského hierarchie (kterážto implikuje stromovou strukturu).

Všechny regulární jazyky splňují nutnou podmínku, tzv. lemma o vkládání, a platí pro ně Myhillova-Nerodova věta.

Odkazy

Související články

Externí odkazy

Obrázky, zvuky či videa k tématu regulární jazyk na Wikimedia Commons