Osmnáctiúhelník

Osmnáctiúhleník, cizím slovem octadecagon či octakaidecagon (z řec. δεκαοχτώ, dekaochtó – osmnáct, a γωνία, gonia – úhel), je mnohoúhelník s osmnácti stranami a vrcholy.

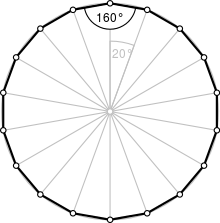
Popis pravidelného osmnáctiúhelníku

Součet středových úhlů pravidelného osmanáctiúhleníku je 360°, jeden středový úhel je tedy ${\frac {360^{\circ }}{18}}=20^{\circ }$ , což je i hodnota každého vnějšího úhlu.

Jeden vnitřní úhel je $180^{\circ }-20^{\circ }$ , součet všech vnitřních úhlů je tedy $160^{\circ }\cdot 18=2880^{\circ }$ .

Je-li α délka strany, pak:

obvod: $P=18\,a$
obsah: $A={\frac {18}{4}}\,a^{2}\cot \left({\frac {\pi }{18}}\right)$

Pravidelný osmnáctiúhelník se všemi možnými spojnicemi vrcholů

minimální poloměr: $H={\frac {2\,A}{P}}={\frac {a}{2}}\cot \left({\frac {\pi }{18}}\right)$
maximální poloměr: $R={\frac {H}{\cos \left({\frac {\pi }{18}}\right)}}={\frac {a}{2\sin \left({\frac {\pi }{18}}\right)}}$

Rýsování

Rýsování pravidelného osmnáctiúhelníku

Pravidelný osmnáctiúhelník nelze narýsovat pouze za pomoci pravítka a kružítka, neboť aby bylo možno daný pravidelný mnohoúhelník narýsovat, musí být všechny jeho liché dělitele být Fermatova čísla ( $F_{n}=2^{2^{\overset {n}{}}}+1$ ).

Osmnáct je dělitelné devíti, což je liché číslo a přitom není Fermanovo. S menší odchylkou (středový úhel se změní z $20^{\circ }$ na $19,99953^{\circ }$ , odchylka tedy $0,00047^{\circ }$ a celkově $0,00846^{\circ }$ ) jej však lze zkonstruovat v 19 krocích:

Utvoříme přímku p.
Narýsujeme kružnici k se středem I, jež se nalézá na přímce p.
Vytvoříme kružnici l se středem v pravém průsečíku kružnice k a přímky p $J=k\cap p$ , jejíž poloměr je shodný s průměrem kružnice k.
Vytvoříme kružnici m se středem v levém průsečíku kružnice k a přímky p $K=k\cap p$ , jejíž poloměr je shodný s průměrem kružnice k.
Narýsujeme přímku q, jež protíná průsečíky kružnic l a m $L=l\cap m$ a $M=l\cap m$ .
Narýsujeme kružnici n, jejíž střed se nachází v průsečíku kružnice k a přímky q $N=k\cap q$ , jejíž průměr je shodný s průměrem kružnice k.
Narýsujeme přímku r, jež protíná průsečíky kružnice k s kružnicí n $O=k\cap n$ a $P=k\cap n$ a je kolmá na přímku p.
Zkonstruujeme kružnici o, jejímž středem je průsečík J a jejíž průměr je totožný s průměrem kružnice k.
Narýsujeme přímku s, jež je kolmá na průsečík J.
Utvoříme kružnici p, která má střed v průsečíku N a průměr totožný s poloměrem kružnice k.
Sestrojíme kružnici q, jejíž střed leží v průsečíku kružnice o a přímky s $R=o\cap s$ a jejíž průměr je stejný jako poloměr kružnice k.
Narýsujeme přímku t, jež je kolmá na přímku q v horním průsečíku kružnice p a přímky q $S=p\cap q$ . Zároveň ji lze popsat jako přímku, jež protíná průsečík S a horní průsečík přímky s a kružnice p.
Narýsujeme přímku u, která protíná bod I a průsečík kružnice n a přímky s $T=n\cap s$ .
Sestrojíme kružnici r, která má střed v průsečíku J a prochází průsečíkem přímky u a kružnice k $U=s\cap k$ .
Vytvoříme přímku v, která prochází oběma průsečíky kružnice r s kružnicí k a je tak kolmá na přímku p.
Zkonstruujeme přímku w, která prochází bodem I a průsečíkem přímky r a v $V=r\cap v$ .
Narýsujeme přímku x, která prochází průsečíkem J a průsečíkem přímky w a t $W=w\cap t$ .
Sestrojíme přímku y, jež prochází bodem I a průsečíkem přímek r a x $X=r\cap x$ .
Přímky p a y svírají úhel α. Vezmeme do kružítka vzdálenost mezi jejich průsečíky s kružnicí k $Y=p\cap k$ a $Z=y\cap k$ a po obvodu kružnice k si uděláme značky, jež následně spojíme.

Při tomto rýsování vytvoříme množství kružnic, průsečíků a přímek. Zde je jejich přehled:

Kružnice: k, l, m, n, o, p, q, r
Průsečíky a body: I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, Y, Z
Přímky: p, q, r, s, t, u, v, w, x, y

Zajímavosti

Obr. 1

Trojúhelník R_A-Q_A-C_B

Pravidelný trojúhelník A18-A17-B3

Zajímavostí je, že pokud k sobě přitiskneme pravidelný osmnáctiúhelník Α a pravidelný devítiúhelník Β (se stejně dlouhými stranami) body A_A a A_B a R_A a B_B a spojíme úsečkou body Q_A a C_B (vrcholu se pojmenovávají proti směru hodinových ručiček), pak vznikne pravidelný rovnostranný trojúhelník R_A-Q_A-C_B.

Obr. 2

Součet vnějšího úhlu A a vnějšího úhlu B musí být 60° (vnitřní úhel pravidelného trojúhelníku). Vnější úhel α je 20°, vnější úhel β tedy musí být $\beta =60^{\circ }-20^{\circ }=40^{\circ }$ . Dává to smysl, neboť osmnáctiúhelník má dvakrát více vrcholů a stran než devítiúhelník.

Osmnáctiúhelníky, devítiúhelníky, kosočtverce a trojúhelníky